Writing your own Gaussian Mixture Model Spark Estimator

Apache Spark is an open source framework for distributed computation. It is particularly adapted for Big Data, effectively speeding up the data analysis and data processing. Spark is particularly known for its very structured architecture allowing customization. One of the key feature of Spark is its Estimators, which is an abstraction of any learning algorithm. In order to get a strong quick jump into the Spark’s ecosystem, we will try implementing our own version of the Gaussian Mixture algorithm for 1-D data.
Apache Spark in a nutshell
As previously stated, Apache Spark is one of the most widely used framework for distributed computation. One of the reasons to its success lays in its very rich and concise high level API for multiple programming languages, such as Scala, Java, Python (with the PySpark library), R and ultimately, SQL. Spark is divided in a multiple layer architecture, ranging from low level, to higher level APIs aimed to a wide range of users.
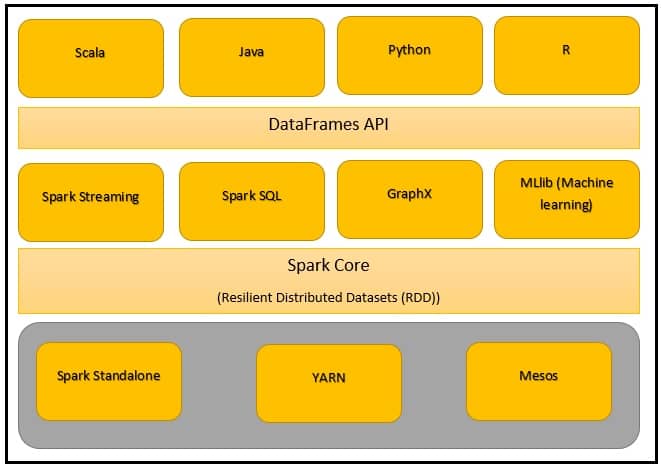
We will review in a litte more details the displayed APIs. Spark is mostly based on in-memory data processing used for analytics, machine learning, ETL (Extract, Transform and Load) and graph processing. One may state that multiple other frameworks use in-memory processing, which is ultimately true, however, Spark’s success is based on multiple other aspects of the framework, which include its speed compared to concurrents, its multi-threaded low level architecture, and a complete and rich support for functionnal programming.
Spark’s beginning
Prior to Spark, the MapReduce was predominent in the field, as it is described as a resilient distributed processing framework (recover from errors and executed on multiple cluster). This programming model have been put into light by Google on their paper: “MapReduce: Simplified Data Processing on Large Clusters” in 2004. MapReduce allowed multiple IT companies that dealt with huge loads of data to perform a more intuitive and faster way of parallelizing their data operations. The model is divided in two parts, as the name state : Map, which is used to map a function to each logical record of the input in order to compute a set of intermediary keys and values, and then, Reduce which applies an operation to a set of values sharing the same key.
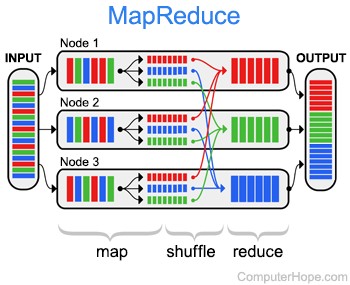
Google’s approach to MapReduce implied three main concepts :
- Data distribution : the input is split into chunks when uploaded to clusters and distributed then replicated over the nodes.
- Distributed computation : As previously stated, a Map function is specified for a couple of key and value and lead to the creation of an intermediary set of key/value, which is then processed by a reduce function. Google’s approach take care of automatically parallelizing programs written using this style on the clusters, with the mapping running on each data block. The result is then transferred to the reducers through a “shuffle and sort” process. Finally, the reducer executes its operation on its node and its chunk of data.
- Fault tolerance : as the data is replicated, each previous step can tolerate failures and recover by switching to another node.
One of the most widely used example of the MapReduce model is the word count, so we won’t be reviewing it, but I will instead directly point to the beginning of this great explanation on DZone.
So you may ask, as MapReduce is scalable, distributed and fault tolerant, why was Spark even developed ?
Well, Spark’s architecture makes it WAY, and I insist on this point, WAY faster than Apache Hadoop, which is built over the MapReduce model. Like 100 times faster. Like comparing Internet Explorer to Chrome. And it is much, much more efficient, due to it’s in-memory processing compared to a disk based processing for MapReduce.
Let’s focus on Spark
Spark main advantage is its capability of handling petabytes of data at a time, given a fair number of nodes on a cluster. For so, Scala offers a wide range of tools and is suited for a number of cases such as :
-
Machine learning : As Spark is built to handle big loads of data, it is particularly suited for Machine Learning, which benefits from a bigger amount of data for increased performance. Spark’s in-memory feature makes the learning signficantly faster than regular frameworks, due to its capability to store the data in memory and run repeated operations over it. The difference in speed, compared to regular framework is even more significant as the data volumne grows. The Spark MLLib provides a full set of of tools for training machine learning algorithms. It is based on the Pipeline abstraction, which is used in popular machine learning tools such as Sickit-Learn in Python, and the principles of Estimators/Transformers, which we will explain in details later, as they are the core of this article.
-
Analytics : Spark’s SQL API provides a high level API for running SQL queries on datasets (basically a higher abstraction of Spark’s RDDs) while maintaining Spark’s performances. On a lower level, one can use all kind of data transformations on RDDs, Datasets or DataFrames, which have the advantage to respond fast.
-
Integration : While I personnaly don’t use Spark for integration, it is however perfectly suited for such tasks involving ETL processes, with a significant performance.
For more informations about Spark, I suggest reading this great ressource by Jacek Laskowski.
Proceeding
Let’s jump to serious stuffs. The main goal of this article is to learn how to implement your own Spark Estimator. I chose to implement the Gaussian Mixture Model algorithm, as it is relatively simple to understand. The Gaussian Mixture Model is natively implemented on Spark MLLib, but the purpose of this article is simply to learn how to implement an Estimator. We will restrain our focus on 1-D data for now in order to simplify stuffs.
Gaussian Mixture Model (GMM)
We will quickly review the working of the GMM algorithm without getting in too much depth. For those willing to understand the algorithm in greater details, refer to this blog post on TowardsDataScience.
GMM is a clustering algorithm where we intend to find clusters of points in the dataset that share common features. Clustering algorithms are an unsupervised learning problem, so we won’t need to bother with providing labels for our data. The GMM algorithm consider that a set of data is constituted of multiple weighted gaussian distribution. The number of cluster defines the number of distributions we are trying to fit, so one needs a prior understanding of the data in order to chose the right value for the number of clusters.
For 1-dim data, we only need to learn one mean and one variance for each distribution. We use a maximum likelihood optimization using the EM algorithm in order to find the optimal parameters, but before this, we need to set initial values :
- The mean and variance can be preset to a predefined value
- The weights are first set to be equal to 1/k (with k being the number of clusters)
The EM algorithm is divided in two phases :
- E : The expectation step, where we compute the likelihood of each observation.
- M : The maximization step, where we update our parameters
The Expectation step
The Probability Density Function for a Gaussian distribution is given by :
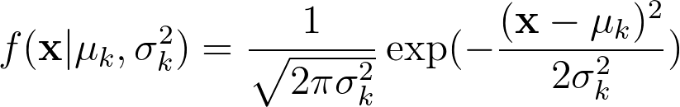
It is calculated for each cluster and each sample of data using the estimated (the prior) values for the mean and variance.
The likelihood is then given by the following formula :
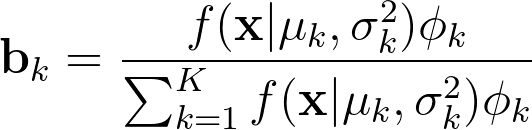
The formula computes the likelihood of a sample Xi to belong to the Kth cluster : the Bayes theorem allows us to get the posterior for the Kth distribution. The parameter Φ is the prior in the formula.
The maximization step
The maximization step simply update the previous parameters for the next iteration :
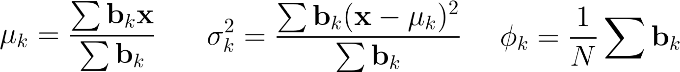
We thus update the mean μₖ, the variance σ₂² and the prior Φₖ for the kth cluster.
The previous steps are repeated until convergence, i.e, where the parameters’s updates becomes insignificant.
Spark’s estimators
Spark’s MLLib implements the concept of Pipelines, which are consistuted of a series of stages, where each stage can either be an Estimator or a Transformer. Transformers apply a transformation on the input dataset, while Estimators produce Models after going through the dataset. Models themselves are transformers, as they provide predictions by transforming the dataset (adding a column with the predictions).
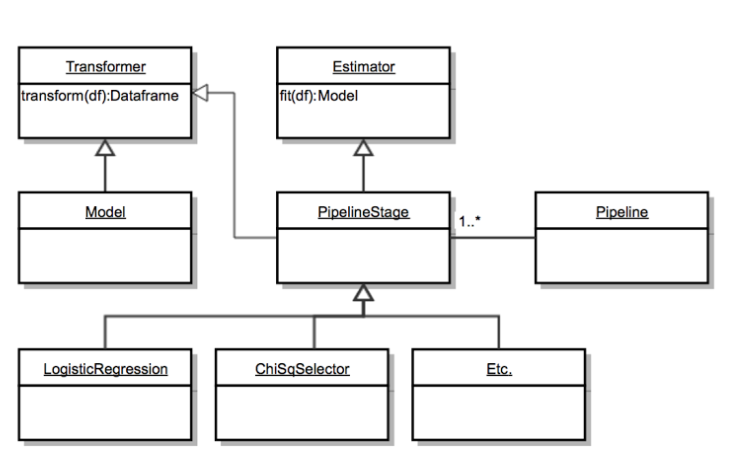
Implementing an Estimator requires us to handle the estimator and model serialization, i.e, the loading and saving.
The Estimator is implemented using the Scala programming language.
Let’s build a kind of roadmap before getting started :
- First, we need to define the different parameters. I am identifying four parameters here :
- K : the number of clusters
- maxIter : the maximum number of iteration for our maximum likelihood optimization algorithm.
- The label column : the 1-dimensional data column of the dataframe
- The prediction column : The column to be created containing the predicted cluster.
-
We then need to define the Model & Estimator, along with their serialization process. We leave the transform and fit methods to fill in the next step.
- We now fill the fit and transform method of the Estimator and the Model respectively.
Ready ? Set ? Go !
Implementation
Let’s start by implementing a trait (interface) containing our parameters. Both the label and prediction column parameters, along with the maxIter parameter, are already implemented by the API, so our trait will only need to extend them. As the K parameter is supposed to be an integer, we use the already built support for Spark integer parameters, which will make it effortless to save and load our model.
trait GaussianMixtureParams extends Params
with HasLabelCol with HasPredictionCol with HasMaxIter {
val k = new IntParam(this, "k", "Number of clusters to train for.")
def setK(value: Int): this.type = set(k -> value)
setDefault(k -> 2) //We set the default value to 2 for the number of clusters
def getK: Int = $(k)
}
This step was quick, but we now need to define the Estimator along with its serialization tools and the Model. Our parameters being of primitive types, we only need to use the default copy and load method provided by the API and accessed from the DefaultParamsWritable and DefaultParamsReadable[T] classes. We then respectively override the copy and load method. Note that the DefaultParamsReadable class is extended by creating a companion object.
We define the setters for our parameters inside the GaussianMixtureEstimator, which itself extends the Estimator abstract class. The Estimator class takes a generic type which correspond to our custom Model. We also extends our GaussianMixtureParams trait to have access to the defined parameters, along with the DefaultParamsWritable class, which requires from us to override the copy() method. As our types are all primitive, we only call the defaultCopy() which take care of the saving.
Extending the Estimator abstract class also requires overriding two methods at least :
-
transformSchema(schema: StructType), which makes the necessary checks to the dataframe (if needed), and return the new schema for the updated dataframe (also if needed). None of these are needed now so we just return the original schema.
-
fit(dataset: Dataset[_]) which implements the learning algorithm (to be filled) and returns a Model.
We also implement the companion object which extends the DefaultReadableParams and override the load method. (A companion object takes the same name as the master class, which can access its properties and methods).
The same structure is used for implementing our Model. We implement our GaussianMixtureNMModel as a case class, as we will save the means, variances and weights in it, which we define as class properties. It extends the raw Model class, which needs our custom model as generic type, along with the parameter traits and saving class. We also need to override the following methods :
-
transformSchema, in this case, we need to append the prediction column to the main schema. We do so by appending a StructType of a StructField of integers to the main schema using the ++ operator.
-
transform(dataset: Dataset[_]), which implements the prediction algorithm and returns a DataFrame containing the predictions.
class GaussianMixtureEstimator(override val uid: String) extends Estimator[GaussianMixtureNMModel]
with GaussianMixtureParams with DefaultParamsWritable {
def this() = this(Identifiable.randomUID("gmm"))
def setLabelCol(value: String): this.type = set(labelCol -> value)
def setPredictionCol(value: String): this.type = set(predictionCol -> value)
def setMaxIter(value: Int): this.type = set(maxIter -> value)
setDefault(maxIter -> 25)
@DeveloperApi
override def transformSchema(schema: StructType): StructType = {
schema
}
override def copy(extra: ParamMap): Estimator[GaussianMixtureNMModel] = defaultCopy(extra)
override def fit(dataset: Dataset[_]): GaussianMixtureNMModel = {
...
}
}
object GaussianMixtureEstimator extends DefaultParamsReadable[GaussianMixtureEstimator] {
override def load(path: String): GaussianMixtureEstimator = super.load(path)
}
case class GaussianMixtureNMModel(override val uid: String,
weightsModel: Array[Double],
variancesModel: Array[Double],
meanModel: Array[Double]
)
extends Model[GaussianMixtureNMModel] with DefaultParamsWritable
with GaussianMixtureParams {
override def copy(extra: ParamMap): GaussianMixtureNMModel = defaultCopy(extra)
override def transformSchema(schema: StructType): StructType = {
StructType(Seq(StructField($(predictionCol), IntegerType, true)).++(schema))
}
override def transform(dataset: Dataset[_]): DataFrame = {
...
}
}
object GaussianMixtureNMModel extends DefaultParamsReadable[GaussianMixtureNMModel] {
override def load(path: String): GaussianMixtureNMModel = super.load(path)
}
Let’s finally fill the learning and prediction methods. We first need to implement a method that compute the PDF. I decided to put it in the GaussianMixtureParams trait as it is both extended by the model and the estimator:
trait GaussianMixtureParams extends Params
with HasLabelCol with HasPredictionCol with HasMaxIter {
...
def pdf(X: List[Double], mean: Double, variance: Double) = {
val s1 = 1 / (Math.sqrt(2 * Math.PI * variance))
val s2 = X.map(value => Math.exp(-1 * (Math.pow(value - mean, 2) / (2 * variance))))
s2.map(s1 * _)
}
}
We then implement the EM algorithm in the fit method :
class GaussianMixtureEstimator(override val uid: String) extends Estimator[GaussianMixtureNMModel]
with GaussianMixtureParams with DefaultParamsWritable {
...
override def fit(dataset: Dataset[_]): GaussianMixtureNMModel = {
val multiplyList = (a: List[Double], b: List[Double]) => {
a.zip(b).map {
case (i, j) => i.toDouble * j.toDouble
}
}
val X = dataset
.select($(labelCol))
.collect.map(r => r.getDouble(0))
.toList
val weights = Array.fill($(k))(1.0)
val means = Random.shuffle(X).take($(k)).toArray
val variances = Seq.fill($(k))(Random.nextDouble).toArray
(0 to $(maxIter)).foreach(_ => {
val likelihood = new ListBuffer[List[Double]]()
val b = new ListBuffer[List[Double]]
(0 until $(k)).foreach(j => {
likelihood.append(pdf(X, means(j), Math.sqrt(variances(j))))
})
(0 until $(k)).foreach(j => {
val updatedLocalLikelihood = likelihood(j).map(_ * weights(j))
val updatedGlobalLikelihood = (0 until $(k)).foldLeft(ListBuffer[List[Double]]())((sum, step) => {
sum.append(likelihood(step).map(_ * weights(step)))
sum
})
val finalGlobalLikelihood = updatedGlobalLikelihood(0).zipWithIndex.map {
case (elem, indice) => {
(1 until $(k)).foldLeft(elem)((sum, indice2) => sum + updatedGlobalLikelihood(indice2)(indice))
}
}
b.append(updatedLocalLikelihood.zip(finalGlobalLikelihood).map {
case (a, b) => a.toDouble / b.toDouble
})
val sumB = b(j).sum
means(j) = multiplyList(b(j), X).sum / sumB
variances(j) = multiplyList(b(j), X.map(x => Math.pow(x - means(j), 2))).sum / sumB
weights(j) = b(j).sum / b(j).length
})
})
GaussianMixtureNMModel(uid, weights, variances, means)
}
}
And finally, the transform method is filled : we need to compute the likelihood for each sample and return the cluster with the highest probability.
case class GaussianMixtureNMModel(override val uid: String,
weightsModel: Array[Double],
variancesModel: Array[Double],
meanModel: Array[Double]
)
extends Model[GaussianMixtureNMModel] with DefaultParamsWritable
with GaussianMixtureParams {
...
override def transform(dataset: Dataset[_]): DataFrame = {
val Y = dataset
.select($(labelCol))
.collect.map(r => r.getDouble(0))
.toList
/* We are doing exactly the same as in the fit method, without the M step */
val likelihood = new ListBuffer[List[Double]]
val b = new ListBuffer[List[Double]]
(0 until $(k)).foreach(j => {
likelihood.append(pdf(Y, meanModel(j), Math.sqrt(variancesModel(j))))
})
(0 until $(k)).foreach(j => {
val updatedLocalLikelihood = likelihood(j).map(_ * weightsModel(j))
val updatedGlobalLikelihood = (0 until $(k)).foldLeft(ListBuffer[List[Double]]())((sum, step) => {
sum.append(likelihood(step).map(_ * weightsModel(step)))
sum
})
val finalGlobalLikelihood = updatedGlobalLikelihood(0).zipWithIndex.map {
case (elem, indice) => {
(1 until $(k)).foldLeft(elem)((sum, indice2) => sum + updatedGlobalLikelihood(indice2)(indice))
}
}
b.append(updatedLocalLikelihood.zip(finalGlobalLikelihood).map {
case (a, b) => a.toDouble / b.toDouble
})
})
val predictions = new ListBuffer[Double]()
Y.zipWithIndex.foreach {
case (_, i) => {
predictions.append(
(0 until $(k)).foldLeft(new ListBuffer[Double]())((list, index) => {
list.append(b(index)(i))
list
})
.zipWithIndex.maxBy(_._1)._2)
}
}
val spark = dataset.sparkSession
/* We get the spark session from the dataset in order to turn the prediction List
into a dataframe */
import spark.implicits._ // Used for implicit dataframe conversion
import org.apache.spark.sql.functions.monotonically_increasing_id
val predictionsDf = spark
.sparkContext
.parallelize(predictions.map(_.toInt + 1))
.toDF($(predictionCol))
.withColumn("id", monotonically_increasing_id)
dataset
.withColumn("id", monotonically_increasing_id())
.join(predictionsDf, "id") //inner join
.drop("id")
.toDF
}
}
AND WE ARE DONE! Testing this is simply done by instanciating the Estimator and calling it’s fit and transform method in a standalone mode, putting it inside a Pipeline :
val estimator = new GaussianMixtureEstimator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setK(3)
estimator.fit(dataset).transform(dataset).show()
The whole code is disponible in my Github repository, or below.
Conclusion
We were able to implement the GMM algorithm from scratch without too much difficulties. The idea was to get a good understanding of the procedure of implementation of a Spark Estimator/Transform. If one wants to implement a transformer, the same procedure as the Model’s implementation is to be followed, except that we won’t need to extend the Model class, but the Transformer class instead.
If you see any mistake or if something is unclear, do not hesitate to comment below and I will do my best to answer :)
Sources
-
https://towardsdatascience.com/gaussian-mixture-modelling-gmm-833c88587c7f
-
https://towardsdatascience.com/how-to-code-gaussian-mixture-models-from-scratch-in-python-9e7975df5252
-
https://mapr.com/blog/spark-101-what-it-what-it-does-and-why-it-matters/
-
https://dzone.com/articles/word-count-hello-word-program-in-mapreduce
Complete code :
import org.apache.parquet.format.IntType
import org.apache.spark.annotation.DeveloperApi
import org.apache.spark.ml.Estimator
import org.apache.spark.ml.param._
import org.apache.spark.ml.param.shared.{HasLabelCol, HasMaxIter, HasPredictionCol}
import org.apache.spark.ml.util.{DefaultParamsReadable, DefaultParamsWritable, Identifiable}
import org.apache.spark.sql.{DataFrame, Dataset}
import org.apache.spark.sql.types._
import org.apache.spark.ml.Model
import scala.collection.mutable.ListBuffer
import scala.util.Random
trait GaussianMixtureParams extends Params
with HasLabelCol with HasPredictionCol with HasMaxIter {
val k = new IntParam(this, "k", "Number of clusters to train for.")
def setK(value: Int): this.type = set(k -> value)
setDefault(k -> 3)
def getK: Int = $(k)
def pdf(X: List[Double], mean: Double, variance: Double) = {
val s1 = 1 / (Math.sqrt(2 * Math.PI * variance))
val s2 = X.map(value => Math.exp(-1 * (Math.pow(value - mean, 2) / (2 * variance))))
s2.map(s1 * _)
}
}
class GaussianMixtureEstimator(override val uid: String) extends Estimator[GaussianMixtureNMModel]
with GaussianMixtureParams with DefaultParamsWritable {
def this() = this(Identifiable.randomUID("gmm"))
def setLabelCol(value: String): this.type = set(labelCol -> value)
def setPredictionCol(value: String): this.type = set(predictionCol -> value)
def setMaxIter(value: Int): this.type = set(maxIter -> value)
setDefault(maxIter -> 25)
@DeveloperApi
override def transformSchema(schema: StructType): StructType = {
schema
}
override def copy(extra: ParamMap): Estimator[GaussianMixtureNMModel] = defaultCopy(extra)
override def fit(dataset: Dataset[_]): GaussianMixtureNMModel = {
val multiplyList = (a: List[Double], b: List[Double]) => {
a.zip(b).map {
case (i, j) => i.toDouble * j.toDouble
}
}
val X = dataset
.select($(labelCol))
.collect.map(r => r.getDouble(0))
.toList
val weights = Array.fill($(k))(1.0)
val means = Random.shuffle(X).take($(k)).toArray
val variances = Seq.fill($(k))(Random.nextDouble).toArray
(0 to $(maxIter)).foreach(_ => {
val likelihood = new ListBuffer[List[Double]]()
val b = new ListBuffer[List[Double]]
(0 until $(k)).foreach(j => {
likelihood.append(pdf(X, means(j), Math.sqrt(variances(j))))
})
(0 until $(k)).foreach(j => {
val updatedLocalLikelihood = likelihood(j).map(_ * weights(j))
val updatedGlobalLikelihood = (0 until $(k)).foldLeft(ListBuffer[List[Double]]())((sum, step) => {
sum.append(likelihood(step).map(_ * weights(step)))
sum
})
val finalGlobalLikelihood = updatedGlobalLikelihood(0).zipWithIndex.map {
case (elem, indice) => {
(1 until $(k)).foldLeft(elem)((sum, indice2) => sum + updatedGlobalLikelihood(indice2)(indice))
}
}
b.append(updatedLocalLikelihood.zip(finalGlobalLikelihood).map {
case (a, b) => a.toDouble / b.toDouble
})
val sumB = b(j).sum
means(j) = multiplyList(b(j), X).sum / sumB
variances(j) = multiplyList(b(j), X.map(x => Math.pow(x - means(j), 2))).sum / sumB
weights(j) = b(j).sum / b(j).length
})
})
GaussianMixtureNMModel(uid, weights, variances, means)
}
}
object GaussianMixtureEstimator extends DefaultParamsReadable[GaussianMixtureEstimator] {
override def load(path: String): GaussianMixtureEstimator = super.load(path)
}
case class GaussianMixtureNMModel(override val uid: String,
weightsModel: Array[Double],
variancesModel: Array[Double],
meanModel: Array[Double]
)
extends Model[GaussianMixtureNMModel] with DefaultParamsWritable
with GaussianMixtureParams {
override def copy(extra: ParamMap): GaussianMixtureNMModel = defaultCopy(extra)
override def transformSchema(schema: StructType): StructType = {
StructType(Seq(StructField($(predictionCol), IntegerType, true)).++(schema))
}
override def transform(dataset: Dataset[_]): DataFrame = {
val Y = dataset
.select($(labelCol))
.collect.map(r => r.getDouble(0))
.toList
val likelihood = new ListBuffer[List[Double]]
val b = new ListBuffer[List[Double]]
(0 until $(k)).foreach(j => {
likelihood.append(pdf(Y, meanModel(j), Math.sqrt(variancesModel(j))))
})
(0 until $(k)).foreach(j => {
val updatedLocalLikelihood = likelihood(j).map(_ * weightsModel(j))
val updatedGlobalLikelihood = (0 until $(k)).foldLeft(ListBuffer[List[Double]]())((sum, step) => {
sum.append(likelihood(step).map(_ * weightsModel(step)))
sum
})
val finalGlobalLikelihood = updatedGlobalLikelihood(0).zipWithIndex.map {
case (elem, indice) => {
(1 until $(k)).foldLeft(elem)((sum, indice2) => sum + updatedGlobalLikelihood(indice2)(indice))
}
}
b.append(updatedLocalLikelihood.zip(finalGlobalLikelihood).map {
case (a, b) => a.toDouble / b.toDouble
})
})
val predictions = new ListBuffer[Double]()
Y.zipWithIndex.foreach {
case (_, i) => {
predictions.append(
(0 until $(k)).foldLeft(new ListBuffer[Double]())((list, index) => {
list.append(b(index)(i))
list
})
.zipWithIndex.maxBy(_._1)._2)
}
}
val spark = dataset.sparkSession
import spark.implicits._
import org.apache.spark.sql.functions.monotonically_increasing_id
val predictionsDf = spark
.sparkContext
.parallelize(predictions.map(_.toInt + 1))
.toDF($(predictionCol))
.withColumn("id", monotonically_increasing_id)
dataset
.withColumn("id", monotonically_increasing_id())
.join(predictionsDf, "id")
.drop("id")
.toDF
}
}
object GaussianMixtureNMModel extends DefaultParamsReadable[GaussianMixtureNMModel] {
override def load(path: String): GaussianMixtureNMModel = super.load(path)
}